1523. Barcelona
Quite recently the City of
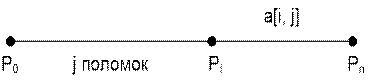
Every tram must go from an
initial point P0 to a final point Pn visiting the intermediate points P1, ..., Pn–1 in this order.
For every 1 ≤ i ≤ n, let Si be the section going from Pi–1 to Pi.
Every such section must be traveled at uniform speed vi, which is chosen by the driver at Pi-1. Let Mi be the maximum possible
speed of the tram at Si,
and assume that the chosen speed is 0 < vi
≤ Mi. Then the
probability of crashing in Si
is vi / Mi. When a crash happens, the
tram uses an efficient recovery system that lasts only 10 seconds. Afterwards,
the tram reaches Pi using
an auxiliary (slow but safe) engine, which provides a speed of 5 meters per
second and guarantees no more crashes in Si.
For instance, assume that
the section length is 300 meters, and that the current maximum speed is 25
meters per second. If the driver chooses to travel at 25 m/s, the tram will
crash for sure. Since the crash can happen anywhere between Pi–1 and Pi, for the sake of
computation we can assume that it will take place exactly in the middle point
(after 150 meters). Therefore, on the average the tram will spend 6 seconds to
reach the middle point, 10 seconds to recover from the crash, and 30 seconds to
reach Pi, for a total of
46 seconds. By contrast, if the tram starts traveling at 15 m/s, with
probability 0.6 it will crash and spend 10 + 10 + 30 = 50 seconds, and with
probability 0.4 it will reach Pi
after 20 seconds without any crash. The average time in this case is thus just
0.6·50 + 0.4·20 = 38 seconds.
When the tram reaches
every Pi, it stops for a
few seconds regardless of having had a crash in Si or not; these few seconds (for simplicity we consider
them to be 0) are enough to (almost) repair the tram: the maximum speed reduces
by 1 m/s after every crash. If we call the initial maximum speed M0,
then we have Mi = M0
– Ci, where 0 ≤ Ci ≤ i – 1 is the total number of crashes
suffered in S1, ..., Si-1.
Write a program that
prints the optimal average travel time given the initial maximum speed and the
length of every section.
Input. Each line corresponds to
one test case and contains the initial maximum speed M0 (a real
number between 5 and 25), the value of n
(an integer number between 1 and M0 – 1), and the length of every
section (each is a real number between 100 and 1000).
Output. For every test case, print the optimal average travel time
with four decimal digits.
|
Sample
input |
Sample
output |
|
25 1 900 25 2 900 900 25 2 305.15 980.76 5 1 1000 |
102.0000 205.0303 150.0000 210.0000 |
SOLUTION
dynamic
programming
Algorithm analysis
Построим формулу
среднего времени для движения трамвая по одному интервалу. Пусть m –
максимально возможная скорость трамвая в начале интервала, s – длина
интервала, x – скорость трамвая на ней. Тогда среднее время движения
равно
f(x) = ![]()
![]() +
+ ![]()
![]()

Найдем скорость x,
для которой это время минимально. Раскроим скобки и сгруппируем:
f(x) = ![]() + x
+ x ![]() –
– ![]()
Производная
равна
f’(x) = ![]() +
+ ![]() =
= ![]()
Приравняем ее к
нулю, и решим уравнение относительно x: ![]() . Получим оптимальную скорость
. Получим оптимальную скорость
x = ![]()
Пусть a[i, j] – минимальное время,
за которое можно доехать с остановки Pi до конца маршрута при
условии, что до этого было j поломок. Очевидно, что a[n, i] = 0.
Обозначим через:
T0 = a[i + 1, j] – оптимальное
время, за которое можно доехать с Pi+1 до конца с j
поломками,
T1 = a[i + 1, j + 1] –
оптимальное время, за которое можно доехать с Pi+1
до конца с j + 1 поломками.
Тогда среднее
время проезда от Pi до конца равно
f(x) = ![]()
![]() +
+ ![]()
![]()
Приравниваем
производную к нулю (решаем уравнение f’(x)
= 0), вычисляем скорость x, для
которой это время будет минимальным. Она равна
x = 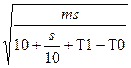
При вычислении a[i, j] следует помнить,
что до Pi было j поломок. Тогда максимально возможная скорость,
которую трамвай может выбрать на Si+1, равна m
= M0 – j. Если вычисленная оптимальная скорость x
будет больше чем M0 – j, то положить x = M0
– j.
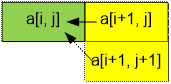
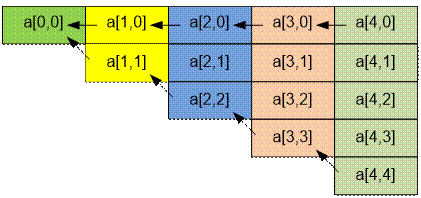
Оптимальное
среднее время, за которое трамвай проедет весь путь, равно a[0, 0]. Вычисление значений массива a идет с конца (сначала вычисляется столбик a[n – 1, i] (0 £ i £ n – 1), потом a[n
– 2, i] (0 £ i £ n – 2) и так далее до a[0, 0]). Каждое значение a[i,
j] пересчитывается через a[i
+ 1, j] и a[i + 1, j
+ 1].
Example
Рассмотрим
второй тест. Данные матрицы a вместе
с оптимальными значениями скоростей x приведены в таблице:
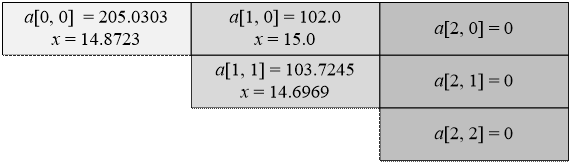
Вычислим a[1, 1]. Оптимальная скорость равна:
x =  =
=  =
= ![]() =
= ![]() ≈ 14.6969
≈ 14.6969
a[1, 1] = ![]()
![]() +
+ 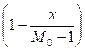
![]() ≈ 103.7245
≈ 103.7245
Вычислим a[1, 0]. Оптимальная скорость равна:
x =  =
=  =
= ![]() = 15
= 15
a[1, 0] = ![]()
![]() +
+ 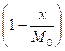
![]() = 102
= 102
Вычислим a[0, 0]. Оптимальная скорость равна:
x =  =
=  =
= ![]() ≈ 14.8723
≈ 14.8723
a[0, 0] = ![]()
![]() +
+ 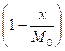
![]() ≈ 205.0303
≈ 205.0303
Algorithm realization
Читаем входные
данные и обнуляем последний столбец матрицы a (a[n, i] = 0, 0 £ i £ n).
while(scanf("%lf
%d",&m0,&n) == 2)
{
for(i = 0; i
< n; i++) scanf("%lf",&s[i]);
for(i = 0; i <= n; i++) a[n][i] = 0;
Динамически пересчитываем
значения i - го столбца через (i + 1) - ый (0 £ i £ n – 1). Данные каждого столбца вычисляем сверху вниз, двигаясь от a[i,
0] до a[i, i].
for(i = n -
1; i >= 0; i--)
for(j = 0;
j <= i; j++)
{
x = sqrt((m0-j) * s[i] /
(10 + s[i]/10 + a[i+1][j+1] - a[i+1][j]));
if (x
> m0 - j) x = m0 - j;
a[i][j] = (x / (m0 - j)) * (s[i]/2/x
+ 10 + s[i]/10 +
a[i+1][j+1]) + (1 - x/(m0-j)) * (s[i]/x + a[i+1][j]);
}
Выводим
результат с 4 десятичными знаками после запятой.
printf("%.4lf\n",a[0][0]);
}